Like I said in my post about memory management on the Jack platform, I love this book.

The Elements of Computing Systems has you build a computer from scratch. By the end you build a platform called Jack, which includes some virtual hardware, an assembler, a virtual machine, a compiler for the Jack language, and an operating system. It’s a lot of fun.

Screen is one of the libraries in the operating system. It has functions that allow you to drawPixels, drawLines, and drawCircles. You can see the screen in the VM emulator.

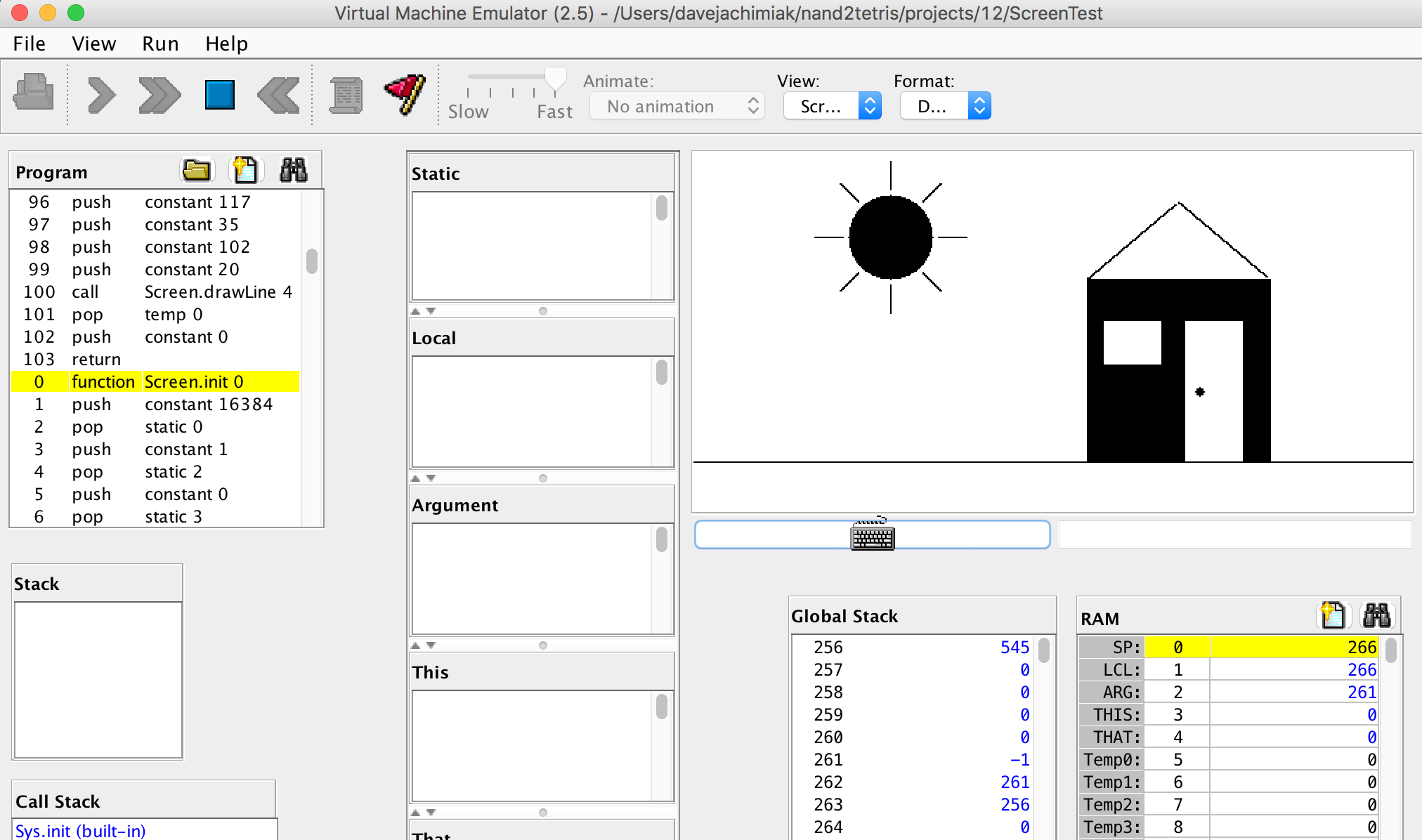
The screen is a Jack “device.” The computer only provides memory space for the device to inspect. The responsibility for changing what the screen looks like based on that memory space belongs to the device. So a contract between the computer and the device needs to exist so that graphics can be displayed correctly. Both device designers and Jack programmers need to know the answer to the question: what do the bit values mean in screen’s memory space?

The contract is:

• The address space for the screen device are from 16384 to 24575, inclusive. (The virtual hardware includes a 16-bit, 23476-address memory space.)
• Each bit in those addresses corresponds to a pixel on the screen. 16-bit addresses means there are 131,072 pixels. There are 512 pixels on the x-axis and 256 pixels on the y-axis.
• If a bit is “on”, or 1, the screen device paints the corresponding pixel black. If it’s “off”, or 0, the screen device paints it white.

We need to keep track of some global variables across the lifespan of the program.

class Screen {
  static int SCREEN, COLOR, BLACK, WHITE;

  function void init() {
    let SCREEN = 16384;
    let BLACK = 1;
    let WHITE = 0;
    let COLOR = BLACK;
    return;
  }

  function void setColor(boolean b) {
    // ...
  }

  function void drawPixel(int x, int y) {
    // ...
  }
}

Screen keeps track of of the current COLOR over the lifetime of a program. We set the default to black.

function void setColor(boolean b) {
  if (b) {
    let COLOR = BLACK;
  } else {
    let COLOR = WHITE;
  }

  return;
}

Screen has a function called setColor(boolean b). If true is passed in, it changes the color to black. Otherwise it changes the color to white.

The current COLOR determines how we’ll calculate changes to screen addresses in drawPixel. We’ll explore that more below.

Screen.drawPixel(int x, int y)

function void drawPixel(int x, int y) {
  var int address, bitPosition, modifier;

  // ...
  
  return;
}

drawPixel takes an (x,y) coordinate. (0,0) is in the upper left corner of the screen. (0,1) is one pixel below, and (1,0) is one pixel to the right. (511,255) is the lower right corner of the screen. Any value for x and y that’s greater than 511 and 255 is invalid, but behavior for those is unspecified.

function void drawPixel(int x, int y) {
  var int address, bitPosition, modifier;

  let address = (y * 32) + (x / 16);

  // ...
  
  return;
}

The first step is to find the address relative to SCREEN that has the mapping to pixel (x,y). The formula is (y * 32) + (x / 16). Let’s break that down.

Some bit in some address between 16384 and 24575 maps to pixel (x,y). The bit is located in some address that has 16 bits. So, for example, pixel (0,0) is in address 16384 and so is pixel (15,0). As we move from address 16384 to the 24575, we’re moving from left to right on the screen and down the screen when we come up against a row’s pixel limit. So, for example, pixel (0,1) is in address 16416, and so is (15,1). Since every row has 512 pixels and there are 16 pixels represented per address, 32 addresses represent each row’s pixels. So we can multiply y * 32 to get the first address of the row we’re looking for. To get the exact address, we divide x by the number of pixels (bits) per address and add it to the first address of the row.

function void drawPixel(int x, int y) {
  var int address, bitPosition, modifier;

  let address = (y * 32) + (x / 16);
  let bitPosition = Screen.modSixteen(x);

  // ...
  
  return;
}

The next step is finding the bit in the address that represents the pixel (x,y). This one’s easy — we just take the remainder of x / 16.

function int modSixteen(int dividend) {
  var int quotient;

  let quotient = dividend / 16;

  return dividend - (quotient * 16);
}

Jack doesn’t have a modulo operator, nor a modulo function in the Math library. Such a function should go there. But since we’re just focusing on Screen right now and the compiler doesn’t allow us to just “open up” the Math library without implementing all of it, we’ll just put modSixteen in Screen.

Finally, we’ll need to somehow modify the address so that we only change pixel (x,y). We’ll get a modifier that we can use on to the address. The modifier will be an integer that has a pixel-corresponding bit of 1 while the rest are 0.

function void drawPixel(int x, int y) {
  var int address, bitPosition, modifier;

  let address = (y * 32) + (x / 16);
  let bitPosition = Screen.modSixteen(x);
  let modifier = Screen.twoToThe(bitPosition);

  // ...
  
  return;
}

function int twoToThe(int i) {
  var int j;

  let j = 1;

  while (i > 0) {
    let j = j * 2;
    let i = i - 1;
  }

  return j;
}

Integers in Jack are stored as 16-bit signed two’s complement. We can shift bits to the left in a two’s complement representation by multiplying it by 2. Using that technique, we can get our modifier by calculating the exponent of 2 to the corresponding, zero-indexed bitPosition.

For example, say that we find pixel (x,y)’s corresponding bit to be in the 0th position of an address. 2 to the 0 is 1, and 1 in 16-bit two’s complement binary is 0000000000000001. If we find that our corresponding bit is in the 4th position, we calculate 2 to the 4 and get 16. 16 in two’s complement binary is 0000000000010000.

(From how we represent binary numbers, the screen device reads address bits from right to left. For example, we read 100 as 00000000001100100 in binary, but the screen will display it as □□■□□■■□□□□□□□□□.)

The challenge is to modify the address to change the pixel (x,y) but not disturb the other pixels. We can do this with some bit arithmetic.

How we’ll do with the modifier and the address depends on the current color.

function void drawPixel(int x, int y) {
  var int address, bitPosition, modifier;

  let address = (y * 32) + (x / 16);
  let bitPosition = Screen.modSixteen(x);
  let modifier = Screen.twoToThe(bitPosition);

  if (COLOR = BLACK) {
    let SCREEN[address] = SCREEN[address] | modifier;
  } else {
    // ...
  }
  
  return;
}

If COLOR is BLACK, we apply the logical OR (|) operation to the address and the modifier. This has the effect of idempotently changing only the modifier’s flipped bit. For example, say the binary value of an address is 1111111100000001 and our modifer is 0000000000000010.

   1111111100000001 <-- current address value
OR 0000000000000010 <-- modifier
------------------
   1111111100000011 <-- new address value

Applying | to the address and the modifier results in 1111111100000011. Now the 2nd pixel in the address has been painted black while leaving everything else the same.

function void drawPixel(int x, int y) {
  var int address, bitPosition, modifier;

  let address = (y * 32) + (x / 16);
  let bitPosition = Screen.modSixteen(x);
  let modifier = Screen.twoToThe(bitPosition);

  if (COLOR = BLACK) {
    let SCREEN[address] = SCREEN[address] | modifier;
  } else {
    let SCREEN[address] = SCREEN[address] & (~modifier);
  }
  
  return;
}

If COLOR is WHITE, we apply the AND (&) operation to the address and a negated version of the modifier. Doing this has the effect of idempotently changing only the negated modifier’s 0 bit in the address. For example, say the binary value of an address is 1111111100000001 and our modifier is 0000000000000001.

    1111111100000001 <-- current address value
AND 1111111111111110 <-- negated modifier
------------------
    1111111100000000 <-- new address value

Applying the negated modifer — 111111111111110 — with AND results in 1111111100000000. Now the 1st pixel in the address has been painted white while leaving the other pixels.